M匹马,N个赛道,求最快前K匹马,至少需要几次比赛?
具体来说,N,M有以下几种常见的情况
M=16,N=4,即16匹马,4个赛道,求前4名,最少进行几次比赛?
M=25,N=5,即25匹马,5个赛道,求前5名,最少进行几次比赛?
M=64,N=4,即64匹马,8个赛道,求前4名,最少进行几次比赛?
M=81,N=4,即81匹马,9个赛道,求前4名,最少进行几次比赛?
N=8,M=4,即64匹马,8个赛道,求前4名,最少进行几次比赛?
拿这个问题来说,用“矩阵画图法”来推导
1)下面是一个矩阵,起初它们都是白色状态,表示没有进行任何比较,次数为0,总共次数为0

2)每一匹马必须至少参与一次比较,否则我是没有办法知道它是前K名,还是K名外,那么我不防每一组进行一次比较,A1-A8一次,B1-B8一次,…,最后H1-H8一次,次数为8,总共次数为8
用黄色来表示:已经参与过比较,但是不确定它是第几名
这里我们不妨假设,每一组中1号马最快,8号马最慢,即A1 < A2 < A3 < … < A8,…,H1 < H2< H3 < … < H8
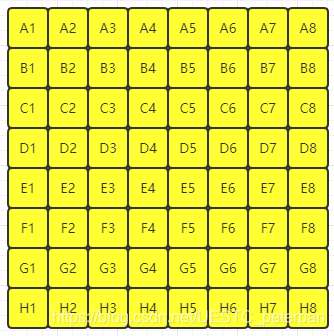
注意,我现在已经能确定每一组中每匹马的速度关系了,但不同组之间的速度关系依然无法确定,因此也无法确定谁是第一名
3)接下来,很显然,我将A1,B1,…,H1进行一次比较,是非常正确的一个做法(否则,请举一个更好的例子),这样子就一定可以确定第一名是谁了,次数为1,总共次数为9
用红色来表示:已经参与过比较,且确定它是第几名
这里我们不妨再假设,A1 < B1 < C1 < … < H1
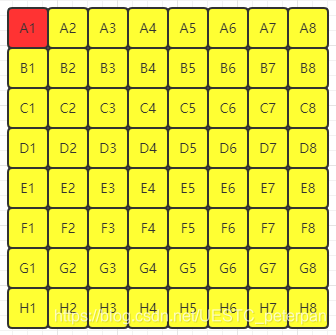
此时我们已经能够确定,每一组中每匹马的速度关系,并且不同组之间最快的马的速度关系,已经可以确定第一名是A1,但还无法确定第二、三、四名是谁
稍等等,仔细观察其实可以发现,有一些马已经可以排除在答案外了,比如A5,因为比它快的马有4匹(A1、A2、A3、A4),它最快也才是第5名,我们要求的是前4名
用蓝色来表示:已经参与过比较,且确定它在答案之外

那么这样一来,突然一下就排除很多马了!并且确定了A1是最快的马,真正需要比较的只有A2、A3、A4、B1、B2、B3、C1、C2、D1这9匹马
81匹马,8个赛道,求出第二、三、四名,需要进行多少次?有的人说2次,有的人说只需要1次,这就是总和答案是11次,还是10次的主要争论原因
不管怎么说,最多为2次,这个肯定没有问题,很明显,你只需要从9匹马中选出8匹马进行一次比较,然后再把剩下的那一匹马参与比较即可,这就是说2次的解法
那么说1次是什么情况呢?说1次其实是用特例来说的,比如我将D1作为那匹不参与第一次比较的马,其余8匹进行比较,并且得到结果是C1是第8名,且已知C1比D1快,那么还有比较D1吗?显然不需要了
不管剩下的9匹马,你选择那一匹作为不参与第一次比较的马,你总能找到一些特例,使得最后一次比较没有必要,但是!同样的,你也一定能找到一些特例,使得最后一次比较必须执行!(我这里就不举例子了,喜欢钻研的朋友可以自己研究研究)
所以,对于网上争论,到底是10次还是11次,其实本质上是对问题中 “至少需要几次比赛” 的 “至少” 这二字定义的争论。如果认为至少含义是“最少”,那么是10次,但如果认为至少含义是“所有情况下最少的最大”,那么就是11次
那么根据我个人的理解,至少含义是“最少”是说不通的,最终答案是11次
好,那么这个问题有没有通解呢?有没有一种解法,可以对任何M、N都可求出一个结果呢?
熟悉图论算法朋友,一定能很快看出上面“矩阵画图法”其实与图论息息相关,图论中是有顶点与边的,每个矩阵元素就是一个顶点,顶点与顶点之间存在一个单向边的关系,from => to 表示 from点的值大于to点的值
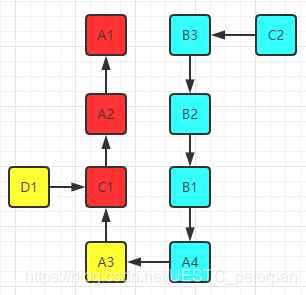
依然以下面这幅图来说

图中存在如下的关系边
- A1 <= A2 <= A3 <= A4
- A1 <= B1 <= B2 <= B3
- A1 <= B1 <= C1 <= C2
- A1 <= B1 <= C1 <= D1
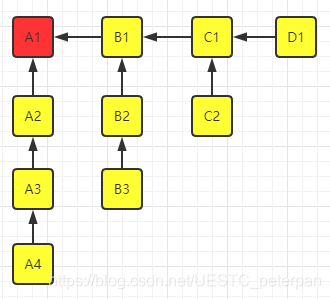
此时我们已经确定了A1是第一名,且可以发现第二名一定在A2与B1中,那么要求剩下的第二、三、四名,不妨就拿D1作为不参与第一次比较的马,其余的8匹马进行比较,来看一下图中的边关系会如何变化
(其实从上面这幅图中也可以看出来,不参与第一次比较的马,还可以选择A4、B3、C2)
我们拿A2、A3、A4、B1、B2、B3、C1、C2进行比较,假设比较结果是:A2 < A3 < A4 < B1 < B2 < B3 < C1 < C2,那么我们就可以画出现在的边关系,如下
- A1 <= A2 <= A3 <= A4 <= B1 <= B2 <= B3 <= C1 <= C2
- C1 <= D1
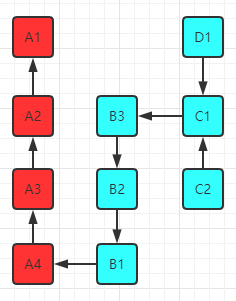
此时,我们是可以确认D1不需要参与第二次比较的了,因为它一定在第4名之外
但是,如果我比较的结果是:A2 < C1 < A3 < A4 < B1 < B2 < B3 < C2 呢?那么边关系就要变为如下
- A1 <= A2 <= C1 <= A3 <= A4 <= B1 <= B2 <= B3 <= C2
- C1 <= D1
此时D1就必须要参与第二次比较了,否则我没法确认到底是D1还是A3是第四名
至此,我们可以推导出通解算法如下
1、将N组赛马进行组内比较,次数为N,总共次数为N
2、将每组的第一名赛马进行比较,次数为1,总共次数为N+1
3、通过1、2建图,得到一个DAG(有向无环图)
4、在图中可以找到第一名的点,即出度为0的顶点(不妨设为A1点)
5、在图中可以找到前K名的点,是唯一到达A1点需要1,2,…,K-1步的点
(唯一很重要,然后到达A1点需要1步是第二名,需要2步是第三名,…)
6、如果K>=M,则寻找结束,否则执行下一步
7、排除掉A1及前K名的点,剩下的点中以到达A1点步数排序,最少最优先
8、排序后,在剩下的点中选择前N名,进行一次比赛,次数+1,并且修改边的指向
9、重新执行5
上面是一个算法思路,实际编码中有一些技巧,比如第5步寻找前K名节点如何寻找?第7步如何对剩下的点进行排序?第8步如何修改边的指向?这都是值得思考的问题。
package raceproblem;
import java.util.*;
public class RaceProblemSolution {
/**
* main方法
*/
public static void main(String[] args) {
RaceProblemSolution solution = new RaceProblemSolution();
solution.randomTest(1, 1, 1);
solution.randomTest(4, 2, 2);
solution.randomTest(9, 3, 3);
solution.randomTest(16, 4, 4);
solution.randomTest(25, 5, 5);
solution.randomTest(64, 8, 4);
solution.randomTest(81, 9, 4);
}
/**
* 检查输入是否合法
*/
void check(int nHorse, int nRace, int nWin) {
if (nHorse <= 0 || nRace <= 0 || nWin <= 0)
throw new RuntimeException("nHorse <= 0 || nRace <= 0 || nWin <= 0");
if (nHorse != nRace * nRace)
throw new RuntimeException("nHorse != nRace * nRace");
if (nHorse < nWin)
throw new RuntimeException("nHorse < nWin");
}
/**
* 生成足够数量次数 arr随机数组,传入solve方法求赛跑次数
*/
void randomTest(int nHorse, int nRace, int nWin) {
check(nHorse, nRace, nWin);
System.out.printf("nHorse: %d, nRace: %d, nWin: %d, ", nHorse, nRace, nWin);
int[] arr = new int[nHorse];
for (int i = 0; i < nHorse; i ++) {
arr[i] = i;
}
Random random = new Random(new Random().nextInt(100));
int min = Integer.MAX_VALUE;
int max = Integer.MIN_VALUE;
for (int i = 0; i < 10000; i ++) {
for (int j = 0; j < nHorse * 5; j ++) {
int t0 = random.nextInt(nHorse);
int t1 = random.nextInt(nHorse);
int t = arr[t0];
arr[t0] = arr[t1];
arr[t1] = t;
}
int res = randomTest(arr, nHorse, nRace, nWin);
min = Integer.min(min, res);
max = Integer.max(max, res);
}
System.out.printf("min: %d, max: %d\n", min, max);
}
/**
* 求赛跑次数的核心方法
*/
int randomTest(int[] arr, int nHorse, int nRace, int nWin) {
// 先将 arr数组 转成 nodes数组
int res = 0;
Node[] nodes = new Node[nHorse];
for (int i = 0; i < nHorse; i ++) {
nodes[i] = new Node(null, arr[i]);
}
// 对每 nRace 匹马进行赛跑,分成 nRace 组
for (int i = 0; i < nHorse; i += nRace) {
Arrays.sort(nodes, i, i + nRace, Comparator.comparingInt(node -> node.speed));
for (int j = i + 1; j < i + nRace; j ++) {
nodes[j].prev = nodes[j-1];
}
}
res += nRace;
// 将 nRace 组中,每组第一名的马进行赛跑,然后计算每匹马的 rank
if (nHorse > 1) {
Node[] nts = new Node[nRace];
for (int i = 0, t = 0; i < nHorse; i += nRace) {
nts[t++] = nodes[i];
}
Arrays.sort(nts, Comparator.comparingInt(node -> node.speed));
for (int i = 1; i < nRace; i ++) {
nts[i].prev = nts[i-1];
}
buildRank(nodes);
Arrays.sort(nodes, Comparator.comparingInt(node -> node.rank));
res += 1;
}
// 循环,直到找到前 nWin 匹马为止
while (true) {
// 判断是否已经找到了前 nWin 匹马
boolean ok = true;
int t = 0;
for (int i = 0; i < nWin; i ++) {
if (nodes[i].rank != i) {
ok = false;
t = i - 1; // 注意是 i-1,改为 i 会 final check error
break;
}
}
if (ok && nWin < nodes.length && nodes[nWin].rank != nWin) {
ok = false;
t = nWin - 1; // 注意是 nWin-1,改为 nWin 会 final check error
}
if (ok)
break;
// 对 nodes[t, t + nRace) 中的马进行一次赛跑
Arrays.sort(nodes, t, t + nRace, Comparator.comparingInt(node -> node.speed));
for (int i = t; i < t + nRace; i ++) {
nodes[i].prev = nodes[i-1];
}
// 重新计算每匹马的 rank
buildRank(nodes);
Arrays.sort(nodes, Comparator.comparingInt(node -> node.rank));
res += 1;
}
// 最终进行一次数据校验,保证结果正确
for (int i = 0; i < nWin; i ++) {
if (nodes[i].speed != i) {
print(nodes);
throw new RuntimeException("final check error");
}
}
return res;
}
/**
* 计算每匹马的 rank
*/
void buildRank(Node[] nodes) {
for (Node node : nodes) {
node.succ.clear();
}
Node root = null;
for (Node node : nodes) {
Node prev = node.prev;
if (prev != null)
prev.succ.add(node);
else
root = node;
}
root.rank = 0;
Queue<Node> q = new LinkedList<>();
q.add(root);
while (!q.isEmpty()) {
Node x = q.poll();
for (Node suc : x.succ) {
suc.rank = x.rank + 1;
q.add(suc);
}
}
}
void print(Node[] nodes) {
for (Node node : nodes) {
Node prev = node.prev;
System.out.printf("(%s, %d, %d), ", prev == null ? "n" : String.valueOf(prev.speed), node.speed, node.rank);
}
System.out.println();
}
/**
* 每匹马的类,也是图论中的顶点类
*/
static class Node {
Node prev; // 前驱节点,最多只有一个
final List<Node> succ; // 所有后继节点
final int speed; // 马的速度,固定
int rank; // 马的排名,会变化
Node(Node prev, int value) {
this.prev = prev;
this.succ = new ArrayList<>();
this.speed = value;
this.rank = 0;
}
};
}输出结果:
nHorse: 1, nRace: 1, nWin: 1, min: 1, max: 1
nHorse: 4, nRace: 2, nWin: 2, min: 4, max: 4
nHorse: 9, nRace: 3, nWin: 3, min: 5, max: 6
nHorse: 16, nRace: 4, nWin: 4, min: 7, max: 8
nHorse: 25, nRace: 5, nWin: 5, min: 8, max: 9
nHorse: 64, nRace: 8, nWin: 4, min: 10, max: 11
nHorse: 81, nRace: 9, nWin: 4, min: 11, max: 11











Comments NOTHING